深く知る。寓意(アレゴリー)と寓意画(ヴァニタス)とは、意味と作品例

こんにちは、岩下 幸圓(イワシタ コウエン)です。今回は寓意(アレゴリー)と寓意画(ヴァニタス)について紹介します。早速ですが、下の画像をご覧ください。

この静物画には、宝石や鎧、赤い布など多くのものが多く描かれています。

一見すると華やかな絵に見えますが、これらにはあるメッセージが込められています。いったい何が込められていると思いますか？

それを解明しながら寓意と寓意画について紹介していきます。それではよろしくお願いします。

そもそも寓意(アレゴリー)って何？

寓意とは広辞苑によると

他の物事にかこつけて、それとなくある意味をほのめかすこと。寓喩「ーを読み取る」

岩波書店『広辞苑　第六版』「寓意」より引用

と記載されています。つまり寓意は、絵の画面に描かれている物体や生物(物事)で、それ以上の物語を意味している、ということです。

では寓意画(ヴァニタス)はどのように誕生したのでしょうか。

寓意画(ヴァニタス)の歴史

16世紀から17世紀になるとフランドルやネールランドなどの北ヨーロッパで静物画が多く描かれました。

しかしそのほとんどはある寓意が込められた寓意画(ヴァニタス)と呼ばれるものでした。

寓意画(ヴァニタス)の背景にはキリスト教の教えがあります。

キリスト教では、天国や地獄、魂の救済など死にまつわる内容が多く、人々の間で死の意識が広まるようになりました。

彼らはメメント・モリ＝死を忘れることなかれ

という警句を作り出しました。

つまり、現世での贅沢や楽しみ、繁栄や富などは空虚でむなしいものである。形あるものは全てなくなってしまう

という意味が込められています。

そのため、寓意画(ヴァニタス)では直接的な死を意味する頭蓋骨、王冠、ガラス、食べ物、金貨など形あるものは死や人生のはかなさを表現しているということです。

ページ冒頭にあった作品のなかにあるものもすべてその意味を込められています。

よく見てみると頭蓋骨が隠れているんですね。是非探してみてください。

もちろん、死のほかにも、愛や節制など他の寓意を表現した寓意画もありますので、作品例で紹介したいと思います。

寓意画の作品例

この作品を見たときに天秤と剣が見られます。天秤には善悪、正義か邪悪かを図り、剣を持っています。これは「正義」という寓意を表現しています。

この作品の左にはコインや装飾品、豪華な器など目に見える富があります。しかし中央の女性はそれよりも右にいる赤ん坊を手に取っています。

これは本当の富についての寓意を表現していると言えます。

この作品は一度が見たことはあるのではないでしょうか。中央の女性がフランス国旗を掲げています。7月革命によって自由を勝ちとったフランス国民を表現しています。自由を寓意していると言ってもよいでしょう。

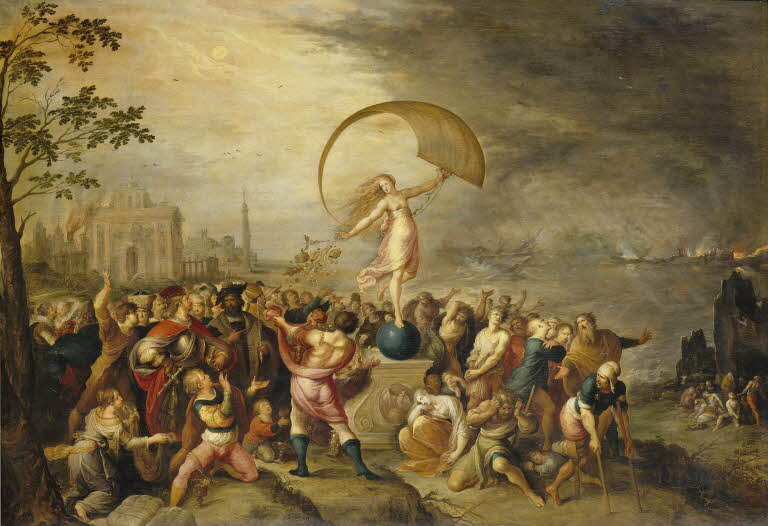
この作品の中央の女性(フォルトゥナ)は不安定な球の上に載っており、さらに手には風をはらんだ布を持っています。これは運命とは不安定で気まぐれなものであるということを寓意しています。

この作品は足元が蛇になった女性？がいます。蛇は邪悪を象徴し、それを翼の生えた女性が踏みつけています。

この作品は邪悪に打ち勝つ＝勝利を寓意しているのではないかと考えられます。

まとめ

寓意(アレゴリー)や寓意画(ヴァニスタ)について紹介しましたが、まだまだ探してみると、沢山の寓意画があります。

この絵画は何を意味しているのか。

そんな風に寓意を探してみるのも面白いですね。

その他にアトリビュートと言われるものもあります。

こちらも補足で読んでいただくとより絵画鑑賞が楽しめます。

最後まで読んでいただきありがとうございました。